My research project centered around Isaac Newton's contributions to calculus, and specifically his discovery of the Fundamental Theorem. The theorem is simply summarized in the image below:
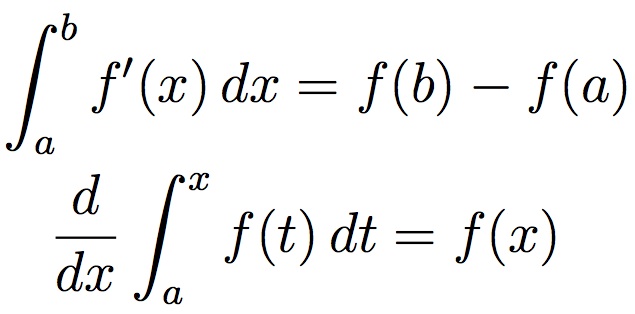
This page will consist of some interactive resources I found and created about the Fundamental Theorem, and more information regarding Isaac Newton. Enjoy!

Before Isaac Newton "invented" calculus in 1665, the word calculus was used to describe all different kinds of mathematics. It is also important to emphasize that while Newton's ideas were monumental in advancing mathematics as a whole, his genius did not result in creating calculus out of thin air. Newton is not called the Father of Calculus because he invented it from nothing, but because in 1665 he made a mathematical discovery that changed the future of calculus forever--a discovery made possible because of those that came before him paving the way.
Isaac Newton was born in a manor in the United Kingdom to a widowed mother, Hannah Ayscough. He came into the world weak and small, and was not expected to live longer than a day. However, despite this and a difficult childhood, Newton grew to live 84 long years and achieved much in this time. He studied the works of Aristotle and other great philosophers and mathematicians to educate himself intensely at Trinity College, Cambridge. One of Newton's first works, "On the Methods of Series and Fluxions", was hugely monumental in the development of modern math, and his basis was centered on what he learned from his studies (Westfall, 2023).
The need for new math was clear: and not just to Isaac Newton. Gottfried Wilhelm Leibniz was a philosopher, scientist, logician, diplomat, lawyer and mathematician who independently discovered Calculus (about 8 years after Newton did) and published his works before Newton published his--resulting in a bitter conflict (sometimes called the "Great Sulk") over who the true "Father of Calculus" is (Mactutor History of Mathematics archive, 2023). Leibniz is widely known for developing the symbols used in mathematics, such as the equal sign, the sign for derivatives, and the integral sign. On the other hand, Newton developed and used the function notation, for example; f(x) = x^2 and f'(x) = 2x.
Newton's proof of this theorem relates to concepts we now know as the Mean Value Theorem, as he took an intermediate rectangle whose area lay between the areas of the inscribed and the circumscribed rectangles to prove that the area of the regions under the graphs could be found using the integration process as he defined it. The additive property of integrals was also key in Newton's proof (Rodriguez, 2023). The Fundamental Theorem opened the mathematical door for intense integration and derivation.
Why is this fundamental to calculus? Because with this theorem in place, there is a guarantee that any continuous function has an anti-derivative, and the entirety of calculus relies on this fact to build upon and use the full power calculus offers (Strang, 2023). This theorem transformed mathematics, and it also had a great impact on physics, astronomy, and many other disciplines.
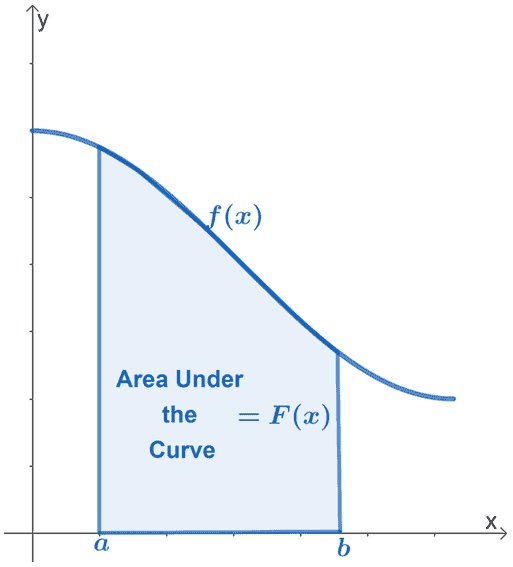
The fundamental theorem is used in many areas, not just math classes! It is used in medicine to determine the growth rate of different substances while combining factors such as temperature and food sources and their relationship to growth. In engineering and physics, the theorem applies to designing space missions with different Earth orbital velocities and gravitational factors that must be determined (UNacademy, 2022). Many more applications of the theorem exist, because not only was it fundamental to calculus itself, but also fundamental to the progression of many studies. Thus we see that Isaac Newton's development of the theorem changed mathematics, and the world.
The fundamental theorem of calculus is a cornerstone of mathematics and a testament to Isaac Newton's profound contributions to calculus as a whole. Newton's work in mathematics, including the development of calculus, has left an indelible mark on the field. Calculus and the fundamental theorem continue to shape our world today, in physics, engineering, economics, and more. In conclusion, the fundamental theorem of calculus, born from the genius of Isaac Newton, stands as a timeless testament to the profound impact of mathematics on our understanding of the world. As we continue to build upon the foundations laid by Newton and others, we are reminded of the enduring legacy of those who dared to explore the limitless boundaries of human knowledge.